Projectile Motion
BlitzMax Forums/BlitzMax Beginners Area/Projectile Motion
| ||
| I'm trying to figure out my trig. I'm deciphering this function... 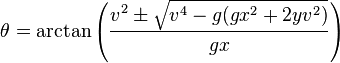 for BlitzMAX. Essentially I need to do 2D Projectile Motion. I need to be able to Graph the points of a projectile based on velocity and angle of launch. Figure out how high it goes, how far, and for how long would be nice too. For graphing purposes I was looking for a function on getting the Y based on X and vise-versa. Even the X,Y by time (frames) would be great. This site was useful http://zonalandeducation.com/mstm/physics/mechanics/curvedMotion/projectileMotion/generalSolution/generalSolution.html But I don't seem to be able to translate it well for Blitz. Because the only values that seem like they might be right is the maximum height, and possibly the distance. But any attempts to make a graphing function fail. I dunno. Any help, or code snippets would be GREAT. Last edited 2010 |
| ||
| Im not sure if this will directly help, but have you checked Warpy's math code blog? http://warpycode.wordpress.com/ |
| ||
| I could be getting this completely wrong, but from the page you posted and what I understand you are asking... the most important part of the link you posted is: Example: In the x direction: vox = vocos(theta) vox = (40.0 m/s)(cos(35 degrees)) vox = (40.0)(0.8191) vox = 32.76 vox = 32.8 m/s In the y direction: voy = vosin(theta) voy = (40.0 m/s)(sin(35 degrees)) voy = (40.0)(0.5735) voy = 22.94 voy = 22.9 m/s So buy knowing the initial speed and angle (40 m/s @ 35 degrees) you get an x velocity of 32.8 m/s and a Y velocity of 22.9 m/s. So to work out how far is has gone in the x direction, it's just a matter of multiplying time (seconds) by 32.8 = metres traveled. This is assuming the x speed is constant - i.e. no wind resistances etc. You will need to mess around with wind resistance etc, and it will be different in the real world. e.g. is there a head wind? a tail win? what is the projectile (golf ball? different to a football?) To work out the y distance. Well assuming you are starting from 0 (ground), then after 1 second it will be 22.9 metres in the air minus any resistance (i.e. gravity which is approx 9.8 metres a second). I've tried to do something similar to what you are doing, but I didn't need this to be exact as what you want. I might have another look at this page tomorrow if the rain continues like it is :D Sorry if this is wrong, I've been drinking and my brain hurts :D |
| ||
| Yes, I've done a few posts on more advanced projectile motion topics, but nothing on the basics. So, the important equations are these: (1) v_t = v_0 + a*t (2) d = v_0 * t + 0.5*a*t^2 The first one gives you the velocity (v_t) after a certain amount of time, and the second one gives you the distance travelled after a certain time. v_0 is the initial velocity. a is the acceleration. There is no acceleration in the x-axis, and the acceleration in the y-axis is equal to the force of gravity (-9.8 m/s^2). Note: the speed of a projectile is a number, like 10 m/s. The velocity is a vector which describes both the speed and the direction the projectile is travelling. Because you're working in 2d, you can break up the velocity into horizontal and vertical bits, and look at them separately. I won't describe the method too much because that page you linked says exactly what I would, and Arabia has helped, so here's some code: Graphics 800,600,0 Const a# = 1 'vertical acceleration. It's positive because screen co-ordinates are the opposite way up to Cartesian graphs, which are what you are taught to use 'on the screen, down is positive and up is negative 'in a Cartesian grid, up is positive and down is negative While Not KeyHit(KEY_ESCAPE) SetColor 0,255,0 DrawLine 0,550,800,550 'draw the ground mx# = MouseX() 'get mouse co-ordinates relative to starting point my# = (550-MouseY()) mx = mx/10 'divide by a constant so this can be used to define the initial velocity (don't want the projectile whizzing off the screen!) my = my/10 an# = ATan2(my,mx) 'work out launch angle speed# = Sqr(mx*mx+my*my) 'work out initial speed SetColor 255,255,255 DrawText "Launch Angle: "+an,0,0 'show the user the launch angle and speed DrawText "Launch Speed: "+speed,0,15 vx0# = speed*Cos(an) 'calculate launch velocity in x and y directions vy0# = -speed*Sin(an) 'we could have just used mx and my, but I'm including this so you can see how to calculate just from an angle and a speed 'we need to flip vy0 because of the screen co-ordinates being the wrong way up tt# = -2*vy0/a 'calculate the total time that the projectile travels dxt# = vx0 * tt 'calculate distance on x-axis that the projectile travels SetColor 0,0,255 DrawText "Total time: "+tt,0,60 'show the user the totals DrawText "Total x-distance: "+dxt,0,75 DrawLine dxt,500,dxt,550 'draw a line showing the landing point topt# = -vy0/a 'might as well work out the maximum height as well. Here's the time the projectile reaches its highest point topy# = vy0*topt + 0.5*a*topt^2 'and here's the maximum height itself. topx# = vx0*topt 'and the corresponding x-distance SetColor 255,255,0 DrawLine topx-50,topy+550,topx+50,topy+550 'draw a line showingthe maximum height DrawText "Maximum height: "+(-topy),0,90 'and show the user the height in pixels 'now plot the path of the projectile. 'We do this by working out, for each point on the x-axis between the launch and the landing, the corresponding height of the projectile SetColor 255,255,255 oy#=0 'oy will keep track of the height of the point before the current point, so we can draw a line between them For dx#=0 To dxt t# = dx/vx0 'calculate the time that the projectile reaches this point dy# = vy0*t + 0.5*a*t^2 'calculate the height of the projectile DrawLine dx,oy+550,dx,dy+550 'draw a line from the old point to the new point oy = dy Next Flip Cls Wend |
| ||
| Wow! That bit of code worked perfectly. I'll try and dissect it to get x,y based on given time. |
| ||
This is a quick and messy way of doing just what you are after (the x,y location at time)SuperStrict Const gravity:Float = -9.8 Local theta:Float ' Angle at which projectile is "projected" Local initialVelocity:Float ' Inital speed at which projectile is "projected" Local velocityX:Float ' The x (Horizontal) velocity of the projectile Local velocityY:Float ' The y (Verticle) velocity of the projectile theta = 35.0 initialVelocity = 40.0 velocityX = initialVelocity * Cos(theta) velocityY = initialVelocity * Sin(theta) Print "Theta:"+theta Print "Initial Velocity:"+initialVelocity Print "x Velocity:"+velocityX Print "y Velocity:"+velocityY Local time : Float ' Print the first 10 seconds of the projectile in increments of approximately one tenth of a second For time = 0 To 10 Step .1 Print "Time:"+time + " X Location:" + velocityX * time + " Y Location:" + (velocityY * time + .5 * gravity * time^2) Next As I said, messy - it doesn't stop showing the location and will actually give you negative results for the y value (i.e. projectile is under ground) if the flight time is less than 10 seconds. You can use the other formula's in Warpy's code to clean it up (by working the total time of flight etc.) or by coding it yourself using the formulas and examples in the original link you posted. p.s. thanks for posting that link, I was actually after these equations - I chucked out my high school math books years ago :D Last edited 2010 |
   |